



Next: Problema de la Mochila
Up: Resolución de Problemas
Previous: Función real multimodal de
Índice General
En este otro ejemplo, propuesto por Castillo en [#!CastilloTESIS!#], se trata de encontrar el óptimo (máximo en este caso) de la siguiente función (marea):
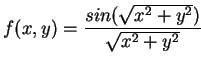 |
|
|
(5.2) |
donde
![$(x,y) \in [0 \ldots 1]$](img43.gif) .
.
Este problema se estudió a fondo en el segundo capítulo de esta memoria, en la sección ![[*]](/home/javi/bin/latex2html/icons.gif/cross_ref_motif.gif) , donde se resolvió de forma secuencial utilizando un programa desarrollado usando la biblioteca OE, por lo que no entraremos en detalles acerca de la función a optimizar.
, donde se resolvió de forma secuencial utilizando un programa desarrollado usando la biblioteca OE, por lo que no entraremos en detalles acerca de la función a optimizar.
Para resolver este otro problema se ha modificado el programa desarrollado en la sección anterior. Simplemente ha habido que cambiar la función de evaluación y la longitud de los individuos (para representar dos números reales en lugar de uno).
La función de evaluación viene dada por la ecuación ![[*]](/home/javi/bin/latex2html/icons.gif/cross_ref_motif.gif) , así simplemente tenemos que implementar dicha función, como una clase descendiente de eoEvalFunc.
, así simplemente tenemos que implementar dicha función, como una clase descendiente de eoEvalFunc.
En las tablas ![[*]](/home/javi/bin/latex2html/icons.gif/cross_ref_motif.gif) y
y ![[*]](/home/javi/bin/latex2html/icons.gif/cross_ref_motif.gif) podemos ver los resultados obtenidos al resolver este problema utilizando las versiones secuencial y paralelas (con las diferentes estrategias de migración) del programa desarrollado.
podemos ver los resultados obtenidos al resolver este problema utilizando las versiones secuencial y paralelas (con las diferentes estrategias de migración) del programa desarrollado.
Tabla:
Resultados (media y desviación estándard) para el problema de la marea utilizando la versión secuencial del programa desarrollado.
| p=100 / g=100 |
Tiempo |
(0.08  0.05 , 0.05 0.05 , 0.05  0.06) 0.06) |
0.28  0.02 0.02 |
| p=400 / g=100 |
Tiempo |
(0.01  0.01 , 0.02 0.01 , 0.02  0.02) 0.02) |
0.89  0.03 0.03 |
| p=800 / g=100 |
Tiempo |
(0.006  0.005 , 0.02 0.005 , 0.02  0.01) 0.01) |
2.008  0.008 0.008 |
| p=1600 / g=100 |
Tiempo |
(0.003  0.003 , 0.004 0.003 , 0.004  0.003) 0.003) |
5.38  0.04 0.04 |
|
Tabla:
Resultados (media y desviación estándard) para el problema de la marea utilizando la versión paralela (con diferentes estrategias de migración) del programa desarrollado.
| Migración |
4 proc. |
Tiempo |
| Simple |
(0.02  0.01 , 0.2 0.01 , 0.2  0.3) 0.3) |
0.41  0.05 0.05 |
| Estrella |
(1.1e-5  1.7e-5 , 7.3e-4 1.7e-5 , 7.3e-4  8.2e-4) 8.2e-4) |
0.86  0.05 0.05 |
| Broadcast |
(3.5e-6  6.7e-6 , 1.7e-6 6.7e-6 , 1.7e-6  3.3e-6) 3.3e-6) |
0.8  0.1 0.1 |
| Anillo |
(2.3e-4  1.7e-4 , 1.8e-3 1.7e-4 , 1.8e-3  3.3e-3) 3.3e-3) |
0.85  0.03 0.03 |
| Migración |
8 proc. |
Tiempo |
| Simple |
(0.03  0.05 , 0.03 0.05 , 0.03  0.02) 0.02) |
0.56  0.05 0.05 |
| Estrella |
(5.1e-5  6.9e-5 , 2.3e-5 6.9e-5 , 2.3e-5  4.2e-5) 4.2e-5) |
0.9  0.1 0.1 |
| Broadcast |
(7e-9  5e-9 , 9e-9 5e-9 , 9e-9  6e-9) 6e-9) |
0.96  0.03 0.03 |
| Anillo |
(6.5e-5  1.2e-4 , 6.2e-5 1.2e-4 , 6.2e-5  5.6e-5) 5.6e-5) |
0.96  0.08 0.08 |
| Migración |
16 proc. |
Tiempo |
| Simple |
(0.02  0.02 , 0.011 0.02 , 0.011  0.005) 0.005) |
0.86  0.05 0.05 |
| Estrella |
(6e-9  6e-9 , 1.1e-7 6e-9 , 1.1e-7  9.4e-8) 9.4e-8) |
1.3  0.1 0.1 |
| Broadcast |
(7e-9  5e-9 , 1.3e-8 5e-9 , 1.3e-8  1.1e-8) 1.1e-8) |
1.71  0.08 0.08 |
| Anillo |
(1.5e-5  1.1e-5 , 2.1e-5 1.1e-5 , 2.1e-5  1.7e-5) 1.7e-5) |
1.2  0.1 0.1 |
|




Next: Problema de la Mochila
Up: Resolución de Problemas
Previous: Función real multimodal de
Índice General
Francisco Javier Garcia Castellano
2000-12-14
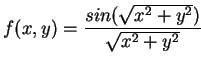
![]() , donde se resolvió de forma secuencial utilizando un programa desarrollado usando la biblioteca OE, por lo que no entraremos en detalles acerca de la función a optimizar.
, donde se resolvió de forma secuencial utilizando un programa desarrollado usando la biblioteca OE, por lo que no entraremos en detalles acerca de la función a optimizar.
![]() , así simplemente tenemos que implementar dicha función, como una clase descendiente de eoEvalFunc.
, así simplemente tenemos que implementar dicha función, como una clase descendiente de eoEvalFunc.
![]() y
y ![]() podemos ver los resultados obtenidos al resolver este problema utilizando las versiones secuencial y paralelas (con las diferentes estrategias de migración) del programa desarrollado.
podemos ver los resultados obtenidos al resolver este problema utilizando las versiones secuencial y paralelas (con las diferentes estrategias de migración) del programa desarrollado.